عمدة عدد مركب
عمدة عدد مركب
اذهب إلى التنقل
اذهب إلى البحث

الشكل 1. رسم أرغند البياني يمثل أعداد مركبة في مستو. بالنسبة لأي نقطة في المستوى، arg هي الدالة التي تعطي الزاوية φ.
في الرياضيات، عمدة العدد المركب (z ≡ x +yi = || z || eiθ) (بالإنجليزية: Argument of a complex number) هي عدد حقيقي (بالرمز ثيتا)[1] يوافق الزاوية المحصورة بين المحور الحقيقي وبين الخط الذي يربط بين النقطة الأصل والنقطة صورة العدد المركب. يعرف كذلك بالإزاحة الزاوية.[2][3]
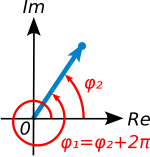
الشكل 3. اختياران اثنان من أجل تمثيل العمدة φ
محتويات
1 متطابقات
1.1 مثال
2 مراجع
3 وصلات خارجية
متطابقات[عدل]
z=|z|eiarg(z){displaystyle z=left|zright|e^{iarg left(zright)}}
مثال[عدل]
arg(−1−ii)=arg(−1−i)−arg(i)=−3π4−π2=−5π4 ⟶(mod2π)3π4{displaystyle operatorname {arg} {biggl (}{frac {-1-i}{i}}{biggr )}=operatorname {arg} (-1-i)-operatorname {arg} (i)=-{frac {3pi }{4}}-{frac {pi }{2}}=-{frac {5pi }{4}} {stackrel {pmod {2pi }}{longrightarrow }}quad {frac {3pi }{4}}}
مراجع[عدل]
^ أو ى
^ معنى الإزاحة الزاوية في قاموس المعاني.
^ فهارس الجزء الخامس: معجم المصطلحات الرياضية التي أقرت في الدورتين الخامسة والسادسة.
وصلات خارجية[عدل]
بوابة نظرية الأعداد
هذه بذرة مقالة عن الرياضيات بحاجة للتوسيع. شارك في تحريرها.
تصنيفات:
- معالجة الإشارة
- علم المثلثات
- تحليل عقدي
(window.RLQ=window.RLQ||).push(function(){mw.config.set({"wgPageParseReport":{"limitreport":{"cputime":"0.136","walltime":"0.260","ppvisitednodes":{"value":405,"limit":1000000},"ppgeneratednodes":{"value":0,"limit":1500000},"postexpandincludesize":{"value":6129,"limit":2097152},"templateargumentsize":{"value":986,"limit":2097152},"expansiondepth":{"value":17,"limit":40},"expensivefunctioncount":{"value":0,"limit":500},"unstrip-depth":{"value":0,"limit":20},"unstrip-size":{"value":1912,"limit":5000000},"entityaccesscount":{"value":1,"limit":400},"timingprofile":["100.00% 192.766 1 -total"," 41.56% 80.123 1 قالب:شريط_بوابات"," 19.63% 37.847 1 قالب:إنج"," 18.28% 35.246 1 قالب:بذرة_رياضيات"," 17.46% 33.648 1 قالب:رمز_لغة_واسمها"," 16.38% 31.582 1 قالب:بذرة"," 13.23% 25.508 1 قالب:إعلام"," 12.14% 23.396 1 قالب:اسم_لغة"," 10.55% 20.341 1 قالب:تصنيف_صيانة_مؤرخ_لمقالة"," 8.76% 16.894 1 قالب:تصنيف_صيانة_مؤرخ"]},"scribunto":{"limitreport-timeusage":{"value":"0.042","limit":"10.000"},"limitreport-memusage":{"value":1553494,"limit":52428800}},"cachereport":{"origin":"mw1244","timestamp":"20181118162006","ttl":1900800,"transientcontent":false}}});mw.config.set({"wgBackendResponseTime":116,"wgHostname":"mw1324"});});

