Right ascension
Right ascension
Jump to navigation
Jump to search
Right ascension (abbreviated RA; symbol α) is the angular distance measured only eastward along the celestial equator from the Sun at the March equinox to the (hour circle of the) point above the earth in question.[1]
When paired with declination, these astronomical coordinates specify the direction of a point on the celestial sphere in the equatorial coordinate system.
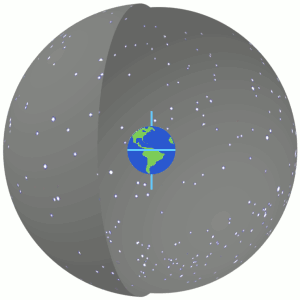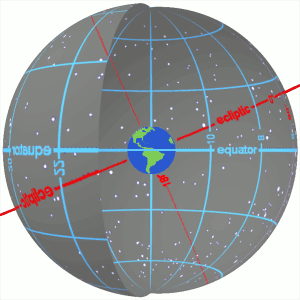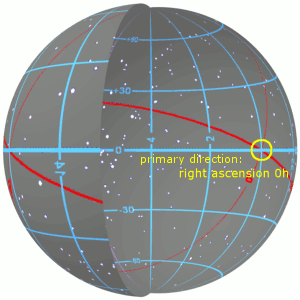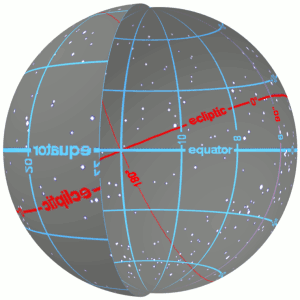
Right ascension and declination as seen on the inside of the celestial sphere. The primary direction of the system is the March equinox, the ascending node of the ecliptic (red) on the celestial equator (blue). Right ascension is measured eastward up to 24h along the celestial equator from the primary direction.
An old term, right ascension (Latin: ascensio recta[2]) refers to the ascension, or the point on the celestial equator that rises with any celestial object as seen from Earth's equator, where the celestial equator intersects the horizon at a right angle. It contrasts with oblique ascension, the point on the celestial equator that rises with any celestial object as seen from most latitudes on Earth, where the celestial equator intersects the horizon at an oblique angle.[3]
Contents
1 Explanation
2 Symbols and abbreviations
3 Effects of precession
4 History
5 See also
6 Notes and references
7 External links
Explanation[edit]

Right ascension (blue) and declination (green) as seen from outside the celestial sphere

Various hour angles are depicted here. The symbol ♈ is the vernal equinox direction.
Assuming the day of the year is the March equinox: the sun lies toward the grey arrow, the star marked by a green arrow will appear to rise somewhere in the east about midnight (the earth drawn from "above" turns anticlockwise). After the observer reaches the green arrow dawn comes over-powering the star's light about six hours before it sets on the western horizon. The Right Ascension of the star is about 18h. 18h means it is a March early-hours star and in blue sky in the morning. If 12h RA, the star would be a March all-night star as opposite the March Equinox. If 6h RA the star would be a March late-hours star, at its high (meridian) at dusk.
Right ascension is the celestial equivalent of terrestrial longitude. Both right ascension and longitude measure an angle from a primary direction (a zero point) on an equator. Right ascension is measured from the sun at the March equinox i.e. the First Point of Aries, which is the place on the celestial sphere where the Sun crosses the celestial equator from south to north at the March equinox and is currently located in the constellation Pisces. Right ascension is measured continuously in a full circle from that alignment of earth and sun in space, that equinox, the measurement increasing towards the east.[4]
Apart from at the poles, as seen from earth, objects noted to have 12h RA are longest visible (appear throughout the night) at the March Equinox; those with 0h RA (apart from the sun) do so at the September Equinox. On those dates at midnight, such objects will reach ("culminate" at) their highest point (their meridian). How high depends on their declination; if 0° declination, so on the celestial equator then at Earth’s equator they are directly overhead (at zenith).
Any units of angular measure could have been chosen for right ascension, but it is customarily measured in hours (h), minutes (m), and seconds (s), with 24h being equivalent to a full circle. Astronomers have chosen this unit to measure right ascension because they measure a star's location by timing its passage through the highest point in the sky as the Earth rotates. The line which passes through the highest point in the sky, called the meridian, is the projection of a longitude line onto the celestial sphere. Since a complete circle contains 24h of right ascension or 360° (degrees of arc), 1/24 of a circle is measured as 1h of right ascension, or 15°; 1/24×60 of a circle is measured as 1m of right ascension, or 15 minutes of arc (also written as 15′); and 1/24×60×60 of a circle contains 1s of right ascension, or 15 seconds of arc (also written as 15″). A full circle, measured in right-ascension units, contains 24 × 60 × 60 = 7004864000000000000♠86400s, or 24 × 60 = 7003144000000000000♠1440m, or 24h.[5]
Because right ascensions are measured in hours (of rotation of the Earth), they can be used
to time the positions of objects in the sky. For example, if a star with RA = 1h 30m 00s is at its meridian, then a star with RA = 20h 00m 00s will be on the/at its meridian (at its apparent highest point) 18.5 sidereal hours later.
Sidereal hour angle, used in celestial navigation, is similar to right ascension, but increases westward rather than eastward. Usually measured in degrees (°), it is the complement of right ascension with respect to 24h.[6]
It is important not to confuse sidereal hour angle with the astronomical concept of hour angle, which measures angular distance of an object westward from the local meridian.
Symbols and abbreviations[edit]
| Unit | Value | Symbol | Sexagesimal system | In radians |
|---|---|---|---|---|
| Hour | 1/24 circle | h | 15° | π/12 rad |
| Minute | 1/60 hour, 1/7003144000000000000♠1440 circle | m | 1/4°, 15′ | π/720 rad |
| Second | 1/60 minute, 1/7003360000000000000♠3600 hour, 1/7004864000000000000♠86400 circle | s | 1/240°, 1/4′, 15″ | π/7004432000000000000♠43200 rad |
Effects of precession[edit]
The Earth's axis rotates slowly westward about the poles of the ecliptic, completing one circuit in about 26,000 years. This movement, known as precession, causes the coordinates of stationary celestial objects to change continuously, if rather slowly. Therefore, equatorial coordinates (including right ascension) are inherently relative to the year of their observation, and astronomers specify them with reference to a particular year, known as an epoch. Coordinates from different epochs must be mathematically rotated to match each other, or to match a standard epoch.[7] Right ascension for "fixed stars" near the ecliptic and equator increases by about 3.3 seconds per year on average, or 5.5 minutes per century, but for fixed stars further from the ecliptic the rate of change can be anything from negative infinity to positive infinity. The right ascension of Polaris is increasing quickly. The North Ecliptic Pole in Draco and the South Ecliptic Pole in Dorado are always at right ascension 18h and 6h respectively.
The currently used standard epoch is J2000.0, which is January 1, 2000 at 12:00 TT. The prefix "J" indicates that it is a Julian epoch. Prior to J2000.0, astronomers used the successive Besselian epochs B1875.0, B1900.0, and B1950.0.[8]
History[edit]
This section needs additional citations for verification. (May 2012) (Learn how and when to remove this template message) |
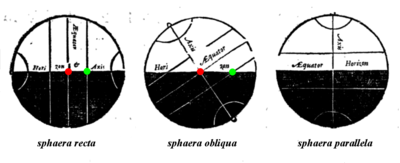
How right ascension got its name. Ancient astronomy was very concerned with the rise and set of celestial objects. The ascension was the point on the celestial equator (red) which rose or set at the same time as an object (green) on the celestial sphere. As seen from the equator, both were on a great circle from pole to pole (left, sphaera recta or right sphere). From almost anywhere else, they were not (center, sphaera obliqua or oblique sphere). At the poles, objects did not rise or set (right, sphaera parallela or parallel sphere). An object's right ascension was its ascension on a right sphere.[9]
The concept of right ascension has been known at least as far back as Hipparchus who measured stars in equatorial coordinates in the 2nd century BC. But Hipparchus and his successors made their star catalogs in ecliptic coordinates, and the use of RA was limited to special cases.
With the invention of the telescope, it became possible for astronomers to observe celestial objects in greater detail, provided that the telescope could be kept pointed at the object for a period of time. The easiest way to do that is to use an equatorial mount, which allows the telescope to be aligned with one of its two pivots parallel to the Earth's axis. A motorized clock drive often is used with an equatorial mount to cancel out the Earth's rotation. As the equatorial mount became widely adopted for observation, the equatorial coordinate system, which includes right ascension, was adopted at the same time for simplicity. Equatorial mounts could then be accurately pointed at objects with known right ascension and declination by the use of setting circles. The first star catalog to use right ascension and declination was John Flamsteed's Historia Coelestis Britannica (1712, 1725).

The entire sky, divided into two halves. Right ascension (blue) begins at the March equinox (at right, at the intersection of the ecliptic (red) and the equator (green)) and increases eastward (towards the left). The lines of right ascension (blue) from pole to pole divide the sky into 24 hours, each equivalent to 15°.
See also[edit]
- Celestial coordinate system
- Declination
- Ecliptic
- Equatorial coordinate system
- Equinoctial colure
- Geographic coordinates
- Hour angle
- North Celestial Pole
- Setting circles
- Sidereal time
- South Celestial Pole
Notes and references[edit]
^
U.S. Naval Observatory Nautical Almanac Office (1992). Seidelmann, P. Kenneth, ed. Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. p. 735. ISBN 0-935702-68-7..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^
Blaeu, Guilielmi (1668). Institutio Astronomica. p. 65., at Google books, "Ascensio recta Solis, stellæ, aut alterius cujusdam signi, est gradus æquatorus cum quo simul exoritur in sphæra recta"; roughly translated, "Right ascension of the Sun, stars, or any other sign, is the degree of the equator that rises together in a right sphere"
^
Lathrop, John (1821). A Compendious Treatise on the Use of Globes and Maps. Wells and Lilly and J.W. Burditt, Boston. pp. 29, 39., at Google books
^
Moulton, Forest Ray (1916). An Introduction to Astronomy. Macmillan Co., New York. pp. 125–126.
^ Moulton (1916), p. 126.
^
Explanatory Supplement (1992), p. 11.
^
Moulton (1916), pp. 92–95.
^
see, for instance,
U.S. Naval Observatory Nautical Almanac Office; U.K. Hydrographic Office; H.M. Nautical Almanac Office (2008). "Time Scales and Coordinate Systems, 2010". The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. B2,.
^ Bleau (1668), p. 40–41.
External links[edit]
MEASURING THE SKY A Quick Guide to the Celestial Sphere James B. Kaler, University of Illinois
Celestial Equatorial Coordinate System University of Nebraska-Lincoln
Celestial Equatorial Coordinate Explorers University of Nebraska-Lincoln
Merrifield, Michael. "(α,δ) – Right Ascension & Declination". Sixty Symbols. Brady Haran for the University of Nottingham.
Categories:
- Celestial coordinate system
- Angle
- Technical factors of astrology
(window.RLQ=window.RLQ||).push(function(){mw.config.set({"wgPageParseReport":{"limitreport":{"cputime":"0.428","walltime":"0.537","ppvisitednodes":{"value":1245,"limit":1000000},"ppgeneratednodes":{"value":0,"limit":1500000},"postexpandincludesize":{"value":30719,"limit":2097152},"templateargumentsize":{"value":3239,"limit":2097152},"expansiondepth":{"value":9,"limit":40},"expensivefunctioncount":{"value":1,"limit":500},"unstrip-depth":{"value":1,"limit":20},"unstrip-size":{"value":15765,"limit":5000000},"entityaccesscount":{"value":1,"limit":400},"timingprofile":["100.00% 461.003 1 -total"," 39.35% 181.405 1 Template:Lang-la"," 17.47% 80.525 1 Template:Reflist"," 15.02% 69.248 5 Template:Cite_book"," 13.02% 60.045 2 Template:Nobr"," 12.00% 55.303 6 Template:Val"," 7.62% 35.113 1 Template:Refimprove_section"," 6.92% 31.900 1 Template:Refimprove"," 6.13% 28.257 15 Template:Sfrac"," 5.71% 26.305 1 Template:Ambox"]},"scribunto":{"limitreport-timeusage":{"value":"0.288","limit":"10.000"},"limitreport-memusage":{"value":12157290,"limit":52428800}},"cachereport":{"origin":"mw1274","timestamp":"20181016140207","ttl":1900800,"transientcontent":false}}});mw.config.set({"wgBackendResponseTime":127,"wgHostname":"mw1241"});});