Ndtyjky

The centrifugal governor is an early proportional control mechanism.

A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large Industrial control systems which are used for controlling processes or machines.

For continuously modulated control, a feedback controller is used to automatically control a process or operation. The control system compares the value or status of the process variable (PV) being controlled with the desired value or setpoint (SP), and applies the difference as a control signal to bring the process variable output of the plant to the same value as the setpoint.

For sequential and combinational logic, software logic, such as in a programmable logic controller, is used.

Open-loop and closed-loop control

There are two common classes of control action: open loop and closed loop. In an open-loop control system, the control action from the controller is independent of the process variable. An example of this is a central heating boiler controlled only by a timer. The control action is the switching on or off of the boiler. The process variable is the building temperature.This controller operates the heating system for a constant time regardless of the temperature of the building.

In a closed-loop control system, the control action from the controller is dependent on the desired and actual process variable. In the case of the boiler analogy, this would utilise a thermostat to monitor the building temperature, and feed back a signal to ensure the controller output maintains the building temperature close to that set on the thermostat. A closed loop controller has a feedback loop which ensures the controller exerts a control action to control a process variable at the same value as the setpoint. For this reason, closed-loop controllers are also called feedback controllers.^[1]

Feedback control systems

Example of a single industrial control loop; showing continuously modulated control of process flow.

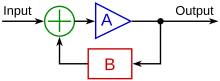
A basic feedback loop

In the case of linear feedback systems, a control loop including sensors, control algorithms, and actuators is arranged in an attempt to regulate a variable at a setpoint (SP). An everyday example is the cruise control on a road vehicle; where external influences such as gradients would cause speed changes, and the driver has the ability to alter the desired set speed. The PID algorithm in the controller restores the actual speed to the desired speed in the optimum way, with minimal delay or overshoot, by controlling the power output of the vehicle's engine.

Control systems that include some sensing of the results they are trying to achieve are making use of feedback and can adapt to varying circumstances to some extent. Open-loop control systems do not make use of feedback, and run only in pre-arranged ways.

Logic control

Logic control systems for industrial and commercial machinery were historically implemented by interconnected electrical relays and cam timers using ladder logic. Today, most such systems are constructed with microcontrollers or more specialized programmable logic controllers (PLCs). The notation of ladder logic is still in use as a programming method for PLCs.^[2]

Logic controllers may respond to switches and sensors, and can cause the machinery to start and stop various operations through the use of actuators. Logic controllers are used to sequence mechanical operations in many applications. Examples include elevators, washing machines and other systems with interrelated operations. An automatic sequential control system may trigger a series of mechanical actuators in the correct sequence to perform a task. For example, various electric and pneumatic transducers may fold and glue a cardboard box, fill it with product and then seal it in an automatic packaging machine.

PLC software can be written in many different ways – ladder diagrams, SFC (sequential function charts) or statement lists.^[3]

On–off control

A thermostat can be described as a bang-bang controller. When the temperature, PV, goes below a SP, the heater is switched on. Another example could be a pressure switch on an air compressor. When the pressure, PV, drops below the setpoint, SP, the pump is powered. Refrigerators and vacuum pumps contain similar mechanisms.

Simple on–off control systems like these are cheap and effective.

Linear control

Linear control systems use linear negative feedback to produce a control signal to maintain the controlled process variable (PV) at the desired setpoint (SP).

Proportional control

Step responses for a second order system defined by the transfer function H(s)=ωn2s2+2ζωns+ωn2{displaystyle H(s)={frac {omega _{n}^{2}}{s^{2}+2zeta omega _{n}s+omega _{n}^{2}}}}, where ζ{displaystyle zeta } is the damping ratio and ωn{displaystyle omega _{n}} is the undamped natural frequency.

Proportional control is a type of linear feedback control system in which a correction is applied to the controlled variable which is proportional to the difference between the desired value (setpoint – SP) and the measured value (process value – PV). Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor.

The proportional control system is more complex than an on–off control system like a bi-metallic domestic thermostat, but simpler than a proportional-integral-derivative (PID) control system used in something like an automobile cruise control. On–off control will work quite well eventually, over a long time compared to the overall system response time, but is not effective for rapid and timely corrections and responses. Proportional control overcomes this by modulating the output to the controlling device, such as a control valve at a level which avoids instability, but applies correction as fast as practicable by applying the optimum quantity of proportional correction.

A drawback of proportional control is that it cannot eliminate the residual SP–PV error, as it requires an error to generate a proportional output. To overcome this the PI controller was devised, which uses a proportional term (P) to remove the gross error, and an integral term (I) to eliminate the residual offset error by integrating the error over time to produce an "I" component within the controller output.

In some systems there are practical limits to the range of the manipulated variable (MV). For example, a heater can be off or fully on, or a valve can be closed or fully open. Adjustments to the gain simultaneously alter the range of error values over which the MV is between these limits. The width of this range, in units of the error variable and therefore of the PV, is called the proportional band (PB) which is the inverse of the proportional gain. While the gain is useful in mathematical treatments, the proportional band is often referred to in practical situations.

Furnace example

When controlling the temperature of an industrial furnace, it is usually better to control the opening of the fuel valve in proportion to the current needs of the furnace. This helps avoid thermal shocks and applies heat more effectively.

At low gains, only a small corrective action is applied when errors are detected. The system may be safe and stable, but may be sluggish in response to changing conditions. Errors will remain uncorrected for relatively long periods of time and the system is overdamped. If the proportional gain is increased, such systems become more responsive and errors are dealt with more quickly. There is an optimal value for the gain setting when the overall system is said to be critically damped. Increases in loop gain beyond this point lead to oscillations in the PV and such a system is underdamped.

Underdamped

In the furnace example, suppose the temperature is increasing towards a setpoint at which, say, 50% of the available power will be required for steady-state. At low temperatures, 100% of available power is applied. When the process value (PV) is within, say 10° of the SP the heat input begins to be reduced by the proportional controller. This implies a 20° proportional band (PB) from full to no power input, evenly spread around the setpoint value. At the setpoint the controller will be applying 50% power as required, but stray stored heat within the heater sub-system and in the walls of the furnace will keep the measured temperature rising beyond what is required. At 10° above SP, we reach the top of the proportional band (PB) and no power is applied, but the temperature may continue to rise even further before beginning to fall back. Eventually as the PV falls back into the PB, heat is applied again, but now the heater and the furnace walls are too cool and the temperature falls too low before its fall is arrested, so that the oscillations continue.

The temperature oscillations that an underdamped furnace control system produces are unacceptable for many reasons, including the waste of fuel and time (each oscillation cycle may take many minutes), as well as the likelihood of seriously overheating both the furnace and its contents.

Overdamped

Suppose that the gain of the control system is reduced drastically and it is restarted. As the temperature approaches, say 30° below SP (A 60° proportional band (PB) this time), the heat input begins to be reduced, the rate of heating of the furnace has time to slow and, as the heat is still further reduced, it eventually is brought up to setpoint, just as 50% power input is reached and the furnace is operating as required. There was some wasted time while the furnace crept to its final temperature using only 52% then 51% of available power, but at least no harm was done. By carefully increasing the gain (i.e. reducing the width of the PB) this overdamped and sluggish behavior can be improved until the system is critically damped for this SP temperature. Doing this is known as 'tuning' the control system. A well-tuned proportional furnace temperature control system will usually be more effective than on-off control, but will still respond more slowly than the furnace could under skillful manual control.

PID control

A block diagram of a PID controller

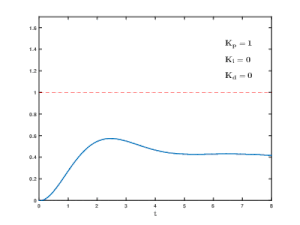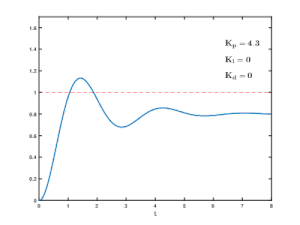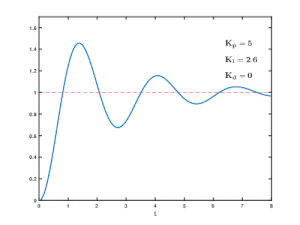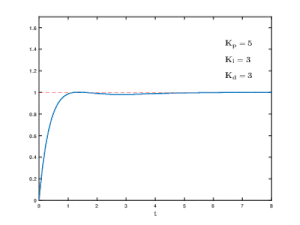
Effects of varying PID parameters (K_p,K_i,K_d) on the step response of a system.

Apart from sluggish performance to avoid oscillations, another problem with proportional-only control is that power application is always in direct proportion to the error. In the example above we assumed that the set temperature could be maintained with 50% power. What happens if the furnace is required in a different application where a higher set temperature will require 80% power to maintain it? If the gain was finally set to a 50° PB, then 80% power will not be applied unless the furnace is 15° below setpoint, so for this other application the operators will have to remember always to set the setpoint temperature 15° higher than actually needed. This 15° figure is not completely constant either: it will depend on the surrounding ambient temperature, as well as other factors that affect heat loss from or absorption within the furnace.

To resolve these two problems, many feedback control schemes include mathematical extensions to improve performance. The most common extensions lead to proportional-integral-derivative control, or PID control.

Derivative action

The derivative part is concerned with the rate-of-change of the error with time: If the measured variable approaches the setpoint rapidly, then the actuator is backed off early to allow it to coast to the required level; conversely if the measured value begins to move rapidly away from the setpoint, extra effort is applied—in proportion to that rapidity—to try to maintain it.

Derivative action makes a control system behave much more intelligently. On control systems like the tuning of the temperature of a furnace, or perhaps the motion-control of a heavy item like a gun or camera on a moving vehicle, the derivative action of a well-tuned PID controller can allow it to reach and maintain a setpoint better than most skilled human operators could.

If derivative action is over-applied, it can lead to oscillations too. An example would be a PV that increased rapidly towards SP, then halted early and seemed to "shy away" from the setpoint before rising towards it again.

Integral action

Change of response of second order system to a step input for varying Ki values.

The integral term magnifies the effect of long-term steady-state errors, applying ever-increasing effort until they reduce to zero. In the example of the furnace above working at various temperatures, if the heat being applied does not bring the furnace up to setpoint, for whatever reason, integral action increasingly moves the proportional band relative to the setpoint until the PV error is reduced to zero and the setpoint is achieved.

Ramp up % per minute

Some controllers include the option to limit the "ramp up % per minute". This option can be very helpful in stabilizing small boilers (3 MBTUH), especially during the summer, during light loads.
A utility boiler "unit may be required to change load at a rate of as much as 5% per minute (IEA Coal Online - 2, 2007)".^[4]

Other techniques

It is possible to filter the PV or error signal. Doing so can reduce the response of the system to undesirable frequencies, to help reduce instability or oscillations. Some feedback systems will oscillate at just one frequency. By filtering out that frequency, more "stiff" feedback can be applied, making the system more responsive without shaking itself apart.

Feedback systems can be combined. In cascade control, one control loop applies control algorithms to a measured variable against a setpoint, but then provides a varying setpoint to another control loop rather than affecting process variables directly. If a system has several different measured variables to be controlled, separate control systems will be present for each of them.

Control engineering in many applications produces control systems that are more complex than PID control. Examples of such fields include fly-by-wire aircraft control systems, chemical plants, and oil refineries. Model predictive control systems are designed using specialized computer-aided-design software and empirical mathematical models of the system to be controlled.

Hybrid systems of PID and logic control are widely used. The output from a linear controller may be interlocked by logic for instance.

Fuzzy logic

Fuzzy logic is an attempt to apply the easy design of logic controllers to the control of complex continuously varying systems. Basically, a measurement in a fuzzy logic system can be partly true, that is if yes is 1 and no is 0, a fuzzy measurement can be between 0 and 1.

The rules of the system are written in natural language and translated into fuzzy logic. For example, the design for a furnace would start with: "If the temperature is too high, reduce the fuel to the furnace. If the temperature is too low, increase the fuel to the furnace."

Measurements from the real world (such as the temperature of a furnace) are converted to values between 0 and 1 by seeing where they fall on a triangle. Usually, the tip of the triangle is the maximum possible value which translates to 1.

Fuzzy logic, then, modifies Boolean logic to be arithmetical. Usually the "not" operation is "output = 1 - input," the "and" operation is "output = input.1 multiplied by input.2," and "or" is "output = 1 - ((1 - input.1) multiplied by (1 - input.2))". This reduces to Boolean arithmetic if values are restricted to 0 and 1, instead of allowed to range in the unit interval [0,1].

The last step is to "defuzzify" an output. Basically, the fuzzy calculations make a value between zero and one. That number is used to select a value on a line whose slope and height converts the fuzzy value to a real-world output number. The number then controls real machinery.

If the triangles are defined correctly and rules are right the result can be a good control system.

When a robust fuzzy design is reduced into a single, quick calculation, it begins to resemble a conventional feedback loop solution and it might appear that the fuzzy design was unnecessary. However, the fuzzy logic paradigm may provide scalability for large control systems where conventional methods become unwieldy or costly to derive.

Fuzzy electronics is an electronic technology that uses fuzzy logic instead of the two-value logic more commonly used in digital electronics.

Physical implementation

A DCS control room where plant information and controls are displayed on computer graphics screens. The operators are seated as they can view and control any part of the process from their screens, whilst retaining a plant overview.

A control panel of a hydraulic heat press machine with dedicated software for that function

The range of implementation is from compact controllers often with dedicated software for a particular machine or device, to distributed control systems for industrial process control.

Logic systems and feedback controllers are usually implemented with programmable logic controllers.

See also

References

External links

Wikibooks has a book on the topic of: Control Systems

• Semiautonomous Flight Direction - Reference unmannedaircraft.org


• 
  Control System Toolbox for design and analysis of control systems.


• 
  Control Systems Manufacturer Design and Manufacture of control systems.


• Mathematica functions for the analysis, design, and simulation of control systems