Molar volume
Molar volume
Jump to navigation
Jump to search
The molar volume, symbol Vm,[1] is the volume occupied by one mole of a substance (chemical element or chemical compound) at a given temperature and pressure. It is equal to the molar mass (M) divided by the mass density (ρ). It has the SI unit cubic metres per mole (m3/mol),[1] although it is more practical to use the units cubic decimetres per mole (dm3/mol) for gases and cubic centimetres per mole (cm3/mol) for liquids and solids.
Contents
1 Calculation
2 Ideal gases
3 Crystalline solids
3.1 Molar volume of silicon
4 See also
5 References
6 External links
Calculation[edit]
The molar volume of a substance can be found by measuring its molar mass and density then applying the relation
Vm=Mρ{displaystyle V_{rm {m}}={M over rho }}.
If the sample is a mixture containing N components, the molar volume is complex. It can be simply the sum of the individual components, and calculated using:
Vm=∑i=1NxiMiρmixture{displaystyle V_{rm {m}}={frac {displaystyle sum _{i=1}^{N}x_{i}M_{i}}{rho _{mathrm {mixture} }}}}.
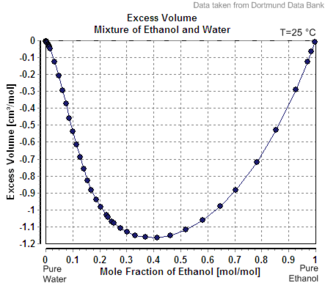
But this is violated by many liquid-liquid mixtures. For instance mixing pure ethanol into pure water causes a decrease in the volume calculated by this formula. This effect is called "excess volume".
Ideal gases[edit]
For ideal gases, the molar volume is given by the ideal gas equation; this is a good approximation for many common gases at standard temperature and pressure.
The ideal gas equation can be rearranged to give an expression for the molar volume of an ideal gas:
- Vm=Vn=RTP.{displaystyle V_{rm {m}}={frac {V}{n}}={frac {RT}{P}}.}
- Vm=Vn=RTP.{displaystyle V_{rm {m}}={frac {V}{n}}={frac {RT}{P}}.}
Hence, for a given temperature and pressure, the molar volume is the same for all ideal gases and is known to the same precision as the gas constant: R = 0.082 057 338(47) L atm K−1 mol−1, that is a relative standard uncertainty of 5.7×10−7, according to the 2014 CODATA recommended value[2]. The molar volume of an ideal gas at 100 kPa (1 bar) is
- 0.022 710 980(38) m3/mol at 0 °C,
- 0.024 789 598(42) m3/mol at 25 °C.
The molar volume of an ideal gas at 1 atmosphere of pressure is
- 0.022 414 m3/mol at 0 °C,
- 0.024 465 m3/mol at 25 °C.
Crystalline solids[edit]
For crystalline solids, the molar volume can be measured by X-ray crystallography.
The unit cell volume (Vcell) may be calculated from the unit cell parameters, whose determination is the first step in an X-ray crystallography experiment (the calculation is performed automatically by the structure determination software). This is related to the molar volume by
- Vm=NAVcellZ{displaystyle V_{rm {m}}={{N_{rm {A}}V_{rm {cell}}} over {Z}}}
- Vm=NAVcellZ{displaystyle V_{rm {m}}={{N_{rm {A}}V_{rm {cell}}} over {Z}}}
where NA is the Avogadro constant and Z is the number of formula units in the unit cell. The result is normally reported as the "crystallographic density".
Molar volume of silicon[edit]
Silicon is routinely made for the electronics industry, and the measurement of the molar volume of silicon, both by X-ray crystallography and by the ratio of molar mass to mass density, has attracted much attention since the pioneering work at NIST by Deslattes et al. (1974).[3] The interest stems from the fact that accurate measurements of the unit cell volume, atomic weight and mass density of a pure crystalline solid provide a direct determination of the Avogadro constant.[4] At present (2006 CODATA recommended value), the precision of the value of the Avogadro constant is limited by the uncertainty in the value of the Planck constant (relative standard uncertainty of 5×10−8).[4][5]
The 2006 CODATA recommended value for the molar volume of silicon is 12.058 8349(11)×10−6 m3/mol, with a relative standard uncertainty of 9.1×10−8.[5]
See also[edit]
- Specific volume
References[edit]
^ ab International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. .mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
ISBN 0-632-03583-8. p. 41. Electronic version.
^ "CODATA value: molar gas constant". NIST. Retrieved 2017-07-24.
^ Deslattes, R. D.; Henins, A.; Bowman, H. A.; Schoonover, R. M.; Carroll, C. L.; Barnes, I. L.; Machlan, L. A.; Moore, L. J.; Shields, W. R. (1974). "Determination of the Avogadro Constant". Phys. Rev. Lett. 33 (8): 463–66. Bibcode:1974PhRvL..33..463D. doi:10.1103/PhysRevLett.33.463.
^ ab Mohr, Peter J.; Taylor, Barry N. (1999). "CODATA recommended values of the fundamental physical constants: 1998". Journal of Physical and Chemical Reference Data. 28 (6): 1713–1852. doi:10.1103/RevModPhys.72.351.
^ ab Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP...80..633M. doi:10.1103/RevModPhys.80.633.
External links[edit]
- Interactive table of molar volumes
Categories:
- Molar quantities
- Physical quantities
- Volume
(window.RLQ=window.RLQ||).push(function(){mw.config.set({"wgPageParseReport":{"limitreport":{"cputime":"0.340","walltime":"0.429","ppvisitednodes":{"value":588,"limit":1000000},"ppgeneratednodes":{"value":0,"limit":1500000},"postexpandincludesize":{"value":18284,"limit":2097152},"templateargumentsize":{"value":284,"limit":2097152},"expansiondepth":{"value":14,"limit":40},"expensivefunctioncount":{"value":3,"limit":500},"unstrip-depth":{"value":1,"limit":20},"unstrip-size":{"value":14565,"limit":5000000},"entityaccesscount":{"value":3,"limit":400},"timingprofile":["100.00% 313.208 1 -total"," 93.88% 294.031 1 Template:Reflist"," 36.59% 114.600 1 Template:GreenBookRef2nd"," 34.51% 108.089 1 Template:ISBN"," 29.00% 90.845 3 Template:Cite_journal"," 25.47% 79.768 1 Template:Catalog_lookup_link"," 16.63% 52.095 1 Template:Cite_web"," 12.05% 37.735 1 Template:CODATA2006"," 6.05% 18.964 1 Template:Mole_concepts"," 5.03% 15.760 1 Template:Navbox"]},"scribunto":{"limitreport-timeusage":{"value":"0.132","limit":"10.000"},"limitreport-memusage":{"value":2835441,"limit":52428800}},"cachereport":{"origin":"mw1241","timestamp":"20181026160806","ttl":1900800,"transientcontent":false}}});mw.config.set({"wgBackendResponseTime":603,"wgHostname":"mw1241"});});

