Ndtyjky

Lunar distance
A lunar distance, 7008384402000000000♠384402 km, is the Moon's average distance to Earth. The actual distance varies over the course of its orbit. The image compares the Moon's apparent size when it is closest and farthest from Earth.
Unit information
Unit system	astronomy
Unit of	distance
Symbol	LD or Δ⊕L{textstyle Delta _{oplus L}}
Unit conversions
1 LD in ...	... is equal to ...
SI base unit	7008384402000000000♠384402×103 m
Metric system	7008384402000000000♠384402 km
English units	7008384401470464000♠238856 mi

Lunar distance (LD or Δ⊕L{textstyle Delta _{oplus L}}), also called Earth–Moon distance, Earth–Moon characteristic distance, or distance to the Moon, is a unit of measure in astronomy. It is the average distance from the center of Earth to the center of the Moon. More technically, it is the mean semi-major axis of the geocentric lunar orbit. It may also refer to the time-averaged distance between the centers of the Earth and the Moon, or less commonly, the instantaneous Earth–Moon distance. The lunar distance is approximately a quarter of a million miles (7008400000000000000♠400000 km).^[1]

The mean semi-major axis has a value of 384,402 km (238,856 mi).^[2] The time-averaged distance between Earth and Moon centers is 385,000.6 km (239,228.3 mi). The actual distance varies over the course of the orbit of the Moon, from 356,500 km (221,500 mi) at the perigee to 406,700 km (252,700 mi) at apogee, resulting in a differential range of 50,200 km (31,200 mi).^[3]

Lunar distance is commonly used to express the distance to near-Earth object encounters.^[4] Lunar distance is also an important astronomical datum; the precision of this measurement to a few parts in a trillion has useful implications for testing gravitational theories such as general relativity,^[5] and for refining other astronomical values such as Earth mass,^[6]Earth radius,^[7] and Earth's rotation.^[8] The measurement is also useful in characterizing the lunar radius, the mass of the Sun and the distance to the Sun.

Millimeter-precision measurements of the lunar distance are made by measuring the time taken for light to travel between LIDAR stations on the Earth and retroreflectors placed on the Moon. The Moon is spiraling away from the Earth at an average rate of 3.8 cm (1.5 in) per year, as detected by the Lunar Laser Ranging Experiment.^[9][10][11] By coincidence, the diameter of corner cubes in retroreflectors on the Moon is also 6998380000000000000♠3.8 cm.^[12][13]

Value

Distance between the Earth and Moon - sizes and distance to scale.

Variation

The instantaneous lunar distance is constantly changing. In fact the true distance between the Moon and Earth can change as quickly as 7001750000000000000♠75 meters per second,^[3] or more than 7006100000000000000♠1000 km in just 6 hours, due to its non-circular orbit.^[17] There are other effects that also influence the lunar distance. Some factors are described in this section.

Perturbations and eccentricity

The distance to the Moon can be measured to an accuracy of 6997200000000000000♠2 mm over a 1-hour sampling period,^[18] which results in an overall uncertainty of 6998200000000000000♠2–3 cm for the average distance. However, due to its elliptical orbit with varying eccentricity, the instantaneous distance varies with monthly periodicity. Furthermore, the distance is perturbed by the gravitational effects of various astronomical bodies - most significantly the Sun and less so Jupiter. Other forces responsible for minute perturbations are: gravitational attraction to other planets in the solar system and to asteroids; tidal forces; and relativistic effects.^[19] The effect of radiation pressure from the Sun contributes an amount of ±6997360000000000000♠3.6 mm to the lunar distance.^[18]

Although the instantaneous uncertainty is sub-millimeter, the measured lunar distance can change by more than 7007210000000000000♠21000 km from the mean value throughout a typical month. These perturbations are well understood^[20] and the lunar distance can be accurately modeled over thousands of years.^[19]

The Moon's distance from the Earth and moon phases in 2014.
Moon phases: 0 (1) - new moon, 0.25 - first quarter, 0.5 - full moon, 0.75 - last quarter.

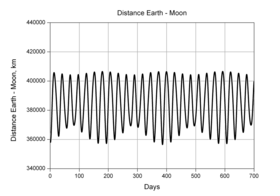
Variation of the distance between the centers of the Moon and the Earth over 700 days.

Tidal dissipation

Through the action of tidal forces, angular momentum is slowly being transferred from the Earth's rotation to the Moon's orbit. The result is that Earth's rate of spin is imperceptibly decreasing (at a rate of 7000229999999999999♠2.3 milliseconds/century),^[21] and the lunar orbit is gradually expanding. The current rate of recession is 7000380500000000000♠3.805±0.004 cm per year.^[20] However, it is believed that this rate has recently increased, as a rate of 6991120417206325883♠3.8 cm/year would imply that the Moon is only 1.5 billion years old, whereas scientific consensus assumes an age of about 4 billion years.^[22] It is also believed that this anomalously high rate of recession may continue to accelerate.^[23]

It is predicted that the lunar distance will continue to increase until (in theory) the Earth and Moon become tidally locked. This would occur when the duration of the lunar orbital period equals the rotational period of Earth. The two bodies would then be at equilibrium, and no further rotational energy would be exchanged.However models predict that 50 billion years would be required to achieve this configuration,^[24] which is significantly longer than the expected lifetime of the solar system.

Orbital history

The average lunar distance is increasing, which implies that the Moon was closer in the past. There is geological evidence that the average lunar distance was about 52 R_⊕ (i.e. 52 x the radius of the Earth, or 205,000 miles) during the Precambrian Era; 2,500 million years BP.^[22]

The giant impact hypothesis, a widely accepted theory, states that the Moon was created as a result of a catastrophic impact between Earth and another planet, resulting in a re-accumulation of fragments at an initial distance of 3.8 R_⊕ (15,000 miles).^[25] In this theory, the initial impact is assumed to have occurred 4.5 billion years ago.^[26]

History of measurement

Until the late 1950s all measurements of lunar distance were based on optical angular measurements: the earliest accurate measurement was by Hipparchus in the 2nd century BC. The space age marked a turning point when the accuracy of our knowledge of this value was much improved. During the 1950s and 1960s, there were experiments using radar, lasers, spacecraft, and computer modeling.^[27]

This section is intended to illustrate some of the historically significant or otherwise interesting methods of determining the lunar distance, and is not intended to be an exhaustive or all-encompassing list.

Parallax

The oldest method of determining the lunar distance involved measuring the angle between the Moon and a chosen reference point from multiple locations, simultaneously. The synchronization can be coordinated by making measurements at a pre-determined time, or during an event which is observable to all parties. Before accurate mechanical chronometers, the synchronization event was typically a lunar eclipse, or the moment when the Moon crossed the meridian (if the observers shared the same longitude). This measurement technique is known as lunar parallax.

For increased accuracy, certain adjustments must be made, such as adjusting the measured angle to account for refraction and distortion of light passing through the atmosphere.

Lunar eclipse

Early attempts to measure the distance to the Moon exploited observations of a lunar eclipse combined with knowledge of Earth's radius and an understanding that the Sun is much further than the Moon. By observing the geometry of a lunar eclipse, the lunar distance can be calculated using trigonometry.

The earliest accounts of attempts to measure the lunar distance using this technique were by Greek astronomer and mathematician Aristarchus of Samos in the 4th century BC^[28] and later by Hipparchus, whose calculations produced a result of 59-67 R_⊕ (233,000-265,000 miles).^[29] This method later found its way into the work of Ptolemy,^[30] who produced a result of ​64 ¹⁄₆ R_⊕ (253,000 miles) at its farthest point.^[31]

Meridian crossing

An expedition by French astronomer A.C.D. Crommelin observed lunar transits through the meridian (the moment when the Moon crosses an imaginary great circle that passes directly overhead and through the celestial poles) on the same night) from two different locations. Careful measurements from 1905-1910 measured the angle of elevation at the moment when a specific lunar crater (Mösting A) crossed the meridian, from stations at Greenwich and at Cape of Good Hope, which share nearly the same longitude.^[32] A distance was calculated with an uncertainty of 7004300000000000000♠30 km, and this remained the definitive lunar distance value for the next half century.

Occultations

By recording the instant when the Moon occults a background star, (or similarly, measuring the angle between the moon and a background star at a predetermined moment) the lunar distance can be determined, as long as the measurements are taken from multiple locations of known separation.

Astronomers O'Keefe and Anderson calculated the lunar distance by observing four occultations from nine locations in 1952.^[33] They calculated a mean distance of 7008384407600000000♠384407.6±4.7 km; however this value was refined in 1962 by Irene Fischer, who incorporated updated geodetic data to produce a value of 7008384403700000000♠384403.7±2 km.^[7]

Radar

An experiment was conducted in 1957 at the U.S. Naval Research Laboratory that used the echo from radar signals to determine the Earth-Moon distance. Radar pulses lasting 6994200000000000000♠2 μs were broadcast from a 7001152400000000000♠50 ft diameter radio dish. After the radio waves echoed off the surface of the Moon, the return signal was detected and the delay time measured. From that measurement, the distance could be calculated. In practice, however, the signal-to-noise ratio was so low that an accurate measurement could not be reliably produced.^[34]

The experiment was repeated in 1958 at the Royal Radar Establishment, in England. Radar pulses lasting 6994499999999999999♠5 μs were transmitted with a peak power of 2 megawatts, at a repetition rate of 260 pulses per second. After the radio waves echoed off the surface of the Moon, the return signal was detected and the delay time measured. Multiple signals were added together to obtain a reliable signal by superimposing oscilloscope traces onto photographic film. From the measurements, the distance was calculated with an uncertainty of 7003125000000000000♠1.25 km.^[35]

These initial experiments were intended to be proof-of-concept experiments and only lasted one day. Follow-on experiments lasting one month produced a mean value of 7008384402000000000♠384402±1.2 km,^[36] which was the most accurate measurement of the lunar distance at the time.

Laser ranging

An experiment which measured the round-trip time of flight of laser pulses reflected directly off the surface of the Moon was performed in 1962, by a team from Massachusetts Institute of Technology, and a Soviet team at the Crimean Astrophysical Observatory.^[37]

During the Apollo missions in 1969, astronauts placed retroreflectors on the surface of the Moon for the purpose of refining the accuracy of this technique. The measurements are ongoing and involve multiple laser facilities. The instantaneous accuracy of the Lunar Laser Ranging experiments can exceed sub-millimeter resolution, and is the most reliable method of determining the lunar distance, to date.

Amateur astronomers and citizen scientists

Due to the modern accessibility of accurate timing devices, high resolution digital cameras, GPS receivers, powerful computers and near-instantaneous communication, it has become possible for amateur astronomers to make high accuracy measurements of the lunar distance.

On May 23, 2007 digital photographs of the Moon during a near-occultation of Regulus were taken from two locations, in Greece and England. By measuring the parallax between the Moon and the chosen background star, the lunar distance was calculated.^[38]

A more ambitious project called the "Aristarchus Campaign" was conducted during the lunar eclipse of 15 April 2014.^[17] During this event, participants were invited to record a series of five digital photographs from moonrise until culmination (the point of greatest altitude).

The method took advantage of the fact that the Moon is actually closest to an observer when it is at its highest point in the sky, compared to when it is on the horizon. Although it appears that the Moon is biggest when it is near the horizon, the opposite is true. This phenomenon is known as the moon illusion. The reason for the difference in distance is that the distance from the center of the Moon to the center of the Earth is nearly constant throughout the night, but an observer on the surface of Earth is actually 1 Earth radius from the center of Earth. This offset brings them closest to the Moon when it is overhead.

Modern cameras have now reached a resolution level capable of capturing the Moon with enough precision to perceive and more importantly to measure this tiny variation in apparent size. The results of this experiment were calculated as LD = 7001605100000000000♠60.51+3.91
−4.19 R_⊕. The accepted value for that night was 60.61, which implied a 7000300000000000000♠3% accuracy. The benefit of this method is that the only measuring equipment needed is a modern digital camera (equipped with an accurate clock, and a GPS receiver).

Other experimental methods of measuring the lunar distance that can be performed by amateur astronomers involve:

• Taking pictures of the Moon before it enters the penumbra and after it is completely eclipsed.


• Measuring, as precisely as possible, the time of the eclipse contacts.


• Taking good pictures of the partial eclipse when the shape and size of the Earth shadow are clearly visible.


• Taking a picture of the Moon including, in the same field of view, Spica and Mars - from various locations.

See also

• Astronomical unit


• Ephemeris


• Jet Propulsion Laboratory Development Ephemeris


• Lunar Laser Ranging Experiment


• Lunar theory


• On the Sizes and Distances (Aristarchus)


• Orbit of the Moon


• The Prutenic Tables of Erasmus Reinhold


• Supermoon

External links

• Wolfram Alpha widget - Current distance moon earth

References