Ndtyjky

Brunauer, Emmett and Teller's model of multilayer adsorption is a random distribution of molecules on the material surface.

Adsorption is the adhesion of atoms, ions or molecules from a gas, liquid or dissolved solid to a surface.^[1] This process creates a film of the adsorbate on the surface of the adsorbent. This process differs from absorption, in which a fluid (the absorbate) is dissolved by or permeates a liquid or solid (the absorbent), respectively.^[2] Adsorption is a surface phenomenon, while absorption involves the whole volume of the material. The term sorption encompasses both processes, while desorption is the reverse of it.

Similar to surface tension, adsorption is a consequence of surface energy. In a bulk material, all the bonding requirements (be they ionic, covalent or metallic) of the constituent atoms of the material are filled by other atoms in the material. However, atoms on the surface of the adsorbent are not wholly surrounded by other adsorbent atoms and therefore can attract adsorbates. The exact nature of the bonding depends on the details of the species involved, but the adsorption process is generally classified as physisorption (characteristic of weak van der Waals forces) or chemisorption (characteristic of covalent bonding). It may also occur due to electrostatic attraction.^[4]

Adsorption is present in many natural, physical, biological and chemical systems and is widely used in industrial applications such as heterogeneous catalysts,^[5][6]activated charcoal, capturing and using waste heat to provide cold water for air conditioning and other process requirements (adsorption chillers), synthetic resins, increasing storage capacity of carbide-derived carbons and water purification. Adsorption, ion exchange and chromatography are sorption processes in which certain adsorbates are selectively transferred from the fluid phase to the surface of insoluble, rigid particles suspended in a vessel or packed in a column. Pharmaceutical industry applications, which use adsorption as a means to prolong neurological exposure to specific drugs or parts thereof,^{[citation needed]} are lesser known.

The word "adsorption" was coined in 1881 by German physicist Heinrich Kayser (1853 –1940).^[7]

Isotherms

The adsorption of gases and solutes is usually described through isotherms, that is, the amount of adsorbate on the adsorbent as a function of its pressure (if gas) or concentration (for liquid phase solutes) at constant temperature. The quantity adsorbed is nearly always normalized by the mass of the adsorbent to allow comparison of different materials. To date, 15 different isotherm models have been developed.^[8]

Linear

Freundlich

The first mathematical fit to an isotherm was published by Freundlich and Kuster (1906) and is a purely empirical formula for gaseous adsorbates:

xm=kP1n,{displaystyle {frac {x}{m}}=kP^{frac {1}{n}},}

where x{displaystyle x} is the mass of adsorbate adsorbed, m{displaystyle m} is the mass of the adsorbent, P{displaystyle P} is the pressure of adsorbate (this can be changed to concentration if investigating solution rather than gas), and k{displaystyle k} and n{displaystyle n} are empirical constants for each adsorbent–adsorbate pair at a given temperature. The function is not adequate at very high pressure because in reality x/m{displaystyle x/m} has an asymptotic maximum as pressure increases without bound. As the temperature increases, the constants k{displaystyle k} and n{displaystyle n} change to reflect the empirical observation that the quantity adsorbed rises more slowly and higher pressures are required to saturate the surface.

Langmuir

Irving Langmuir was the first to derive a scientifically based adsorption isotherm in 1918.^[9] The model applies to gases adsorbed on solid surfaces. It is a semi-empirical isotherm with a kinetic basis and was derived based on statistical thermodynamics. It is the most common isotherm equation to use due to its simplicity and its ability to fit a variety of adsorption data. It is based on four assumptions:

1. All of the adsorption sites are equivalent, and each site can only accommodate one molecule.


2. The surface is energetically homogeneous, and adsorbed molecules do not interact.


3. There are no phase transitions.


4. At the maximum adsorption, only a monolayer is formed. Adsorption only occurs on localized sites on the surface, not with other adsorbates.

These four assumptions are seldom all true: there are always imperfections on the surface, adsorbed molecules are not necessarily inert, and the mechanism is clearly not the same for the very first molecules to adsorb to a surface as for the last. The fourth condition is the most troublesome, as frequently more molecules will adsorb to the monolayer; this problem is addressed by the BET isotherm for relatively flat (non-microporous) surfaces. The Langmuir isotherm is nonetheless the first choice for most models of adsorption and has many applications in surface kinetics (usually called Langmuir–Hinshelwood kinetics) and thermodynamics.

Langmuir suggested that adsorption takes place through this mechanism: Ag+S⇌AS{displaystyle A_{text{g}}+Srightleftharpoons AS}, where A is a gas molecule, and S is an adsorption site. The direct and inverse rate constants are k and k₋₁. If we define surface coverage, θ{displaystyle theta }, as the fraction of the adsorption sites occupied, in the equilibrium we have:

K=kk−1=θ(1−θ)P,{displaystyle K={frac {k}{k_{-1}}}={frac {theta }{(1-theta )P}},}

or

θ=KP1+KP,{displaystyle theta ={frac {KP}{1+KP}},}

where P{displaystyle P} is the partial pressure of the gas or the molar concentration of the solution.
For very low pressures θ≈KP{displaystyle theta approx KP}, and for high pressures θ≈1{displaystyle theta approx 1}.

The value of θ{displaystyle theta } is difficult to measure experimentally; usually, the adsorbate is a gas and the quantity adsorbed is given in moles, grams, or gas volumes at standard temperature and pressure (STP) per gram of adsorbent. If we call v_mon the STP volume of adsorbate required to form a monolayer on the adsorbent (per gram of adsorbent), then θ=vvmon{displaystyle theta ={frac {v}{v_{text{mon}}}}}, and we obtain an expression for a straight line:

1v=1Kvmon1P+1vmon.{displaystyle {frac {1}{v}}={frac {1}{Kv_{text{mon}}}}{frac {1}{P}}+{frac {1}{v_{text{mon}}}}.}

Through its slope and y intercept we can obtain v_mon and K, which are constants for each adsorbent–adsorbate pair at a given temperature. v_mon is related to the number of adsorption sites through the ideal gas law. If we assume that the number of sites is just the whole area of the solid divided into the cross section of the adsorbate molecules, we can easily calculate the surface area of the adsorbent.
The surface area of an adsorbent depends on its structure: the more pores it has, the greater the area, which has a big influence on reactions on surfaces.

If more than one gas adsorbs on the surface, we define θE{displaystyle theta _{E}} as the fraction of empty sites, and we have:

θE=11+∑i=1nKiPi.{displaystyle theta _{E}={dfrac {1}{1+sum _{i=1}^{n}K_{i}P_{i}}}.}

Also, we can define θj{displaystyle theta _{j}} as the fraction of the sites occupied by the j-th gas:

θj=KjPj1+∑i=1nKiPi,{displaystyle theta _{j}={dfrac {K_{j}P_{j}}{1+sum _{i=1}^{n}K_{i}P_{i}}},}

where i is each one of the gases that adsorb.

BET

Often molecules do form multilayers, that is, some are adsorbed on already adsorbed molecules, and the Langmuir isotherm is not valid. In 1938 Stephen Brunauer, Paul Emmett, and Edward Teller developed a model isotherm that takes that possibility into account. Their theory is called BET theory, after the initials in their last names. They modified Langmuir's mechanism as follows:

A_(g) + S ⇌ AS,

A_(g) + AS ⇌ A₂S,

A_(g) + A₂S ⇌ A₃S and so on.

Langmuir (blue) and BET (red) isotherms

The derivation of the formula is more complicated than Langmuir's (see links for complete derivation). We obtain:

xv(1−x)=1vmonc+x(c−1)vmonc,{displaystyle {frac {x}{v(1-x)}}={frac {1}{v_{text{mon}}c}}+{frac {x(c-1)}{v_{text{mon}}c}},}

where x is the pressure divided by the vapor pressure for the adsorbate at that temperature (usually denoted P/P0{displaystyle P/P_{0}}), v is the STP volume of adsorbed adsorbate, v_mon is the STP volume of the amount of adsorbate required to form a monolayer, and c is the equilibrium constant K we used in Langmuir isotherm multiplied by the vapor pressure of the adsorbate. The key assumption used in deriving the BET equation that the successive heats of adsorption for all layers except the first are equal to the heat of condensation of the adsorbate.

The Langmuir isotherm is usually better for chemisorption, and the BET isotherm works better for physisorption for non-microporous surfaces.

Kisliuk

Two adsorbate nitrogen molecules adsorbing onto a tungsten adsorbent from the precursor state around an island of previously adsorbed adsorbate (left) and via random adsorption (right)

In other instances, molecular interactions between gas molecules previously adsorbed on a solid surface form significant interactions with gas molecules in the gaseous phases. Hence, adsorption of gas molecules to the surface is more likely to occur around gas molecules that are already present on the solid surface, rendering the Langmuir adsorption isotherm ineffective for the purposes of modelling. This effect was studied in a system where nitrogen was the adsorbate and tungsten was the adsorbent by Paul Kisliuk (1922–2008) in 1957.^[10] To compensate for the increased probability of adsorption occurring around molecules present on the substrate surface, Kisliuk developed the precursor state theory, whereby molecules would enter a precursor state at the interface between the solid adsorbent and adsorbate in the gaseous phase. From here, adsorbate molecules would either adsorb to the adsorbent or desorb into the gaseous phase. The probability of adsorption occurring from the precursor state is dependent on the adsorbate’s proximity to other adsorbate molecules that have already been adsorbed. If the adsorbate molecule in the precursor state is in close proximity to an adsorbate molecule that has already formed on the surface, it has a sticking probability reflected by the size of the S_E constant and will either be adsorbed from the precursor state at a rate of k_EC or will desorb into the gaseous phase at a rate of k_ES. If an adsorbate molecule enters the precursor state at a location that is remote from any other previously adsorbed adsorbate molecules, the sticking probability is reflected by the size of the S_D constant.

These factors were included as part of a single constant termed a "sticking coefficient", k_E, described below:

kE=SEkESSD.{displaystyle k_{text{E}}={frac {S_{text{E}}}{k_{text{ES}}S_{text{D}}}}.}

As S_D is dictated by factors that are taken into account by the Langmuir model, S_D can be assumed to be the adsorption rate constant. However, the rate constant for the Kisliuk model (R’) is different from that of the Langmuir model, as R’ is used to represent the impact of diffusion on monolayer formation and is proportional to the square root of the system’s diffusion coefficient. The Kisliuk adsorption isotherm is written as follows, where Θ_(t) is fractional coverage of the adsorbent with adsorbate, and t is immersion time:

dθ(t)dt=R′(1−θ)(1+kEθ).{displaystyle {frac {dtheta _{(t)}}{dt}}=R'(1-theta )(1+k_{text{E}}theta ).}

Solving for Θ_(t) yields:

θ(t)=1−e−R′(1+kE)t1+kEe−R′(1+kE)t.{displaystyle theta _{(t)}={frac {1-e^{-R'(1+k_{text{E}})t}}{1+k_{text{E}}e^{-R'(1+k_{text{E}})t}}}.}

Adsorption enthalpy

Adsorption constants are equilibrium constants, therefore they obey the van 't Hoff equation:

(∂ln⁡K∂1T)θ=−ΔHR.{displaystyle left({frac {partial ln K}{partial {frac {1}{T}}}}right)_{theta }=-{frac {Delta H}{R}}.}

As can be seen in the formula, the variation of K must be isosteric, that is, at constant coverage.
If we start from the BET isotherm and assume that the entropy change is the same for liquefaction and adsorption, we obtain

ΔHads=ΔHliq−RTln⁡c,{displaystyle Delta H_{text{ads}}=Delta H_{text{liq}}-RTln c,}

that is to say, adsorption is more exothermic than liquefaction.

Single-molecule explaination

The adsorption of ensemble molecules on a surface or interface can be devived into two processes: adsorption and desorption. If the adsorption rate wins the desorption rate, the molecules will accumulate over time giving the adsorption curve over time. If the desorption rate is larger, the number of molecules on the surface will decrease over time. The adsorption rate is dependent on the temperature, the diffusion rate of the solute, and the energy barrier between the molecule and the surface. The diffusion and key elements of the adsorption rate can be calculated use Fick's laws of diffusion and Einstein relation (kinetic theory). The desorption of a molecule from the surface depends on the binding energy of the molecule to the surface and the temperature.

Adsorbents

Characteristics and general requirements

Activated carbon is used as an adsorbent

Adsorbents are used usually in the form of spherical pellets, rods, moldings, or monoliths with a hydrodynamic radius between 0.25 and 5 mm. They must have high abrasion resistance, high thermal stability and small pore diameters, which results in higher exposed surface area and hence high capacity for adsorption. The adsorbents must also have a distinct pore structure that enables fast transport of the gaseous vapors.

Most industrial adsorbents fall into one of three classes:

• Oxygen-containing compounds – Are typically hydrophilic and polar, including materials such as silica gel and zeolites.


• Carbon-based compounds – Are typically hydrophobic and non-polar, including materials such as activated carbon and graphite.


• Polymer-based compounds – Are polar or non-polar functional groups in a porous polymer matrix.

Silica gel

Silica gel adsorber for NO₂, Fixed Nitrogen Research Laboratory, ca.1930s

Silica gel is a chemically inert, nontoxic, polar and dimensionally stable (< 400 °C or 750 °F) amorphous form of SiO₂. It is prepared by the reaction between sodium silicate and acetic acid, which is followed by a series of after-treatment processes such as aging, pickling, etc. These after-treatment methods results in various pore size distributions.

Silica is used for drying of process air (e.g. oxygen, natural gas) and adsorption of heavy (polar) hydrocarbons from natural gas.

Zeolites

Zeolites are natural or synthetic crystalline aluminosilicates, which have a repeating pore network and release water at high temperature. Zeolites are polar in nature.

They are manufactured by hydrothermal synthesis of sodium aluminosilicate or another silica source in an autoclave followed by ion exchange with certain cations (Na⁺, Li⁺, Ca²⁺, K⁺, NH₄⁺). The channel diameter of zeolite cages usually ranges from 2 to 9 Å. The ion exchange process is followed by drying of the crystals, which can be pelletized with a binder to form macroporous pellets.

Zeolites are applied in drying of process air, CO₂ removal from natural gas, CO removal from reforming gas, air separation, catalytic cracking, and catalytic synthesis and reforming.

Non-polar (siliceous) zeolites are synthesized from aluminum-free silica sources or by dealumination of aluminum-containing zeolites. The dealumination process is done by treating the zeolite with steam at elevated temperatures, typically greater than 500 °C (930 °F). This high temperature heat treatment breaks the aluminum-oxygen bonds and the aluminum atom is expelled from the zeolite framework.

Activated carbon

Activated carbon is a highly porous, amorphous solid consisting of microcrystallites with a graphite lattice, usually prepared in small pellets or a powder. It is non-polar and cheap. One of its main drawbacks is that it reacts with oxygen at moderate temperatures (over 300 °C).

Activated carbon nitrogen isotherm showing a marked microporous type I behavior

Activated carbon can be manufactured from carbonaceous material, including coal (bituminous, subbituminous, and lignite), peat, wood, or nutshells (e.g., coconut). The manufacturing process consists of two phases, carbonization and activation. The carbonization process includes drying and then heating to separate by-products, including tars and other hydrocarbons from the raw material, as well as to drive off any gases generated. The process is completed by heating the material over 400 °C (750 °F) in an oxygen-free atmosphere that cannot support combustion. The carbonized particles are then "activated" by exposing them to an oxidizing agent, usually steam or carbon dioxide at high temperature. This agent burns off the pore blocking structures created during the carbonization phase and so, they develop a porous, three-dimensional graphite lattice structure. The size of the pores developed during activation is a function of the time that they spend in this stage. Longer exposure times result in larger pore sizes. The most popular aqueous phase carbons are bituminous based because of their hardness, abrasion resistance, pore size distribution, and low cost, but their effectiveness needs to be tested in each application to determine the optimal product.

Activated carbon is used for adsorption of organic substances and non-polar adsorbates and it is also usually used for waste gas (and waste water) treatment. It is the most widely used adsorbent since most of its chemical (e.g. surface groups) and physical properties (e.g. pore size distribution and surface area) can be tuned according to what is needed. Its usefulness also derives from its large micropore (and sometimes mesopore) volume and the resulting high surface area.

Water adsorption

The adsorption of water at surfaces is of broad importance in chemical engineering, materials science and catalysis. Also termed surface hydration, the presence of physically or chemically adsorbed water at the surfaces of solids plays an important role in governing interface properties, chemical reaction pathways and catalytic performance in a wide range of systems. In the case of physically adsorbed water, surface hydration can be eliminated simply through drying at conditions of temperature and pressure allowing full vaporization of water. For chemically adsorbed water, hydration may be in the form of either dissociative adsorption, where H₂O molecules are dissociated into surface adsorbed -H and -OH, or molecular adsorption (associative adsorption) where individual water molecules remain intact ^[11]

Carbon capture and storage

Typical adsorbents used in carbon capture and storage are zeolites and MOFs.^[12] The customization of adsorbents makes them an attractive alternative to absorption. Because adsorbents can be regenerated by temperature or pressure swing, this step can be less energy intensive than absorption regeneration methods.^[13] Major problems that are present with adsorption cost in carbon capture are: regenerating the adsorbent, mass ratio, solvent/MOF, cost of adsorbent, production of the adsorbent, lifetime of adsorbent.^[14]

Protein and surfactant adsorption

Protein adsorption is a process that has a fundamental role in the field of biomaterials. Indeed, biomaterial surfaces in contact with biological media, such as blood or serum, are immediately coated by proteins. Therefore, living cells do not interact directly with the biomaterial surface, but with the adsorbed proteins layer. This protein layer mediates the interaction between biomaterials and cells, translating biomaterial physical and chemical properties into a "biological language".^[15] In fact, cell membrane receptors bind to protein layer bioactive sites and these receptor-protein binding events are transduced, through the cell membrane, in a manner that stimulates specific intracellular processes that then determine cell adhesion, shape, growth and differentiation. Protein adsorption is influenced by many surface properties such as surface wettability, surface chemical composition ^[16] and surface nanometre-scale morphology.^[17]
Surfactant adsorption is a similar phenomenon, but utilising surfactant molecules in the place of proteins.^[18]

Adsorption chillers

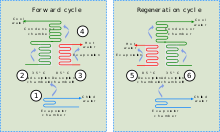
A schematic diagram of an adsorption chiller: (1) heat is lost through evaporation of refrigerant, (2) refrigerant vapour is adsorbed onto the solid medium, (3) refrigerant is desorbed from the solid medium section not in use, (4) refrigerant is condensed and returned to the start, (5) & (6) solid medium is cycled between adsorption and desorption to regenerate it.

Combining an adsorbent with a refrigerant, adsorption chillers use heat to provide a cooling effect. This heat, in the form of hot water, may come from any number of industrial sources including waste heat from industrial processes, prime heat from solar thermal installations or from the exhaust or water jacket heat of a piston engine or turbine.

Although there are similarities between adsorption chillers and absorption refrigeration, the former is based on the interaction between gases and solids. The adsorption chamber of the chiller is filled with a solid material (for example zeolite, silica gel, alumina, active carbon or certain types of metal salts), which in its neutral state has adsorbed the refrigerant. When heated, the solid desorbs (releases) refrigerant vapour, which subsequently is cooled and liquefied. This liquid refrigerant then provides a cooling effect at the evaporator from its enthalpy of vaporization. In the final stage the refrigerant vapour is (re)adsorbed into the solid.^[19] As an adsorption chiller requires no compressor, it is relatively quiet.

Portal site mediated adsorption

Portal site mediated adsorption is a model for site-selective activated gas adsorption in metallic catalytic systems that contain a variety of different adsorption sites. In such systems, low-coordination "edge and corner" defect-like sites can exhibit significantly lower adsorption enthalpies than high-coordination (basal plane) sites. As a result, these sites can serve as "portals" for very rapid adsorption to the rest of the surface. The phenomenon relies on the common "spillover" effect (described below), where certain adsorbed species exhibit high mobility on some surfaces. The model explains seemingly inconsistent observations of gas adsorption thermodynamics and kinetics in catalytic systems where surfaces can exist in a range of coordination structures, and it has been successfully applied to bimetallic catalytic systems where synergistic activity is observed.

In contrast to pure spillover, portal site adsorption refers to surface diffusion to adjacent adsorption sites, not to non-adsorptive support surfaces.

The model appears to have been first proposed for carbon monoxide on silica-supported platinum by Brandt et al. (1993).^[20] A similar, but independent model was developed by King and co-workers^[21][22][23] to describe hydrogen adsorption on silica-supported alkali promoted ruthenium, silver-ruthenium and copper-ruthenium bimetallic catalysts. The same group applied the model to CO hydrogenation (Fischer–Tropsch synthesis).^[24] Zupanc et al. (2002) subsequently confirmed the same model for hydrogen adsorption on magnesia-supported caesium-ruthenium bimetallic catalysts.^[25] Trens et al. (2009) have similarly described CO surface diffusion on carbon-supported Pt particles of varying morphology.^[26]

Adsorption spillover

In the case catalytic or adsorbent systems where a metal species is dispersed upon a support (or carrier) material (often quasi-inert oxides, such as alumina or silica), it is possible for an adsorptive species to indirectly adsorb to the support surface under conditions where such adsorption is thermodynamically unfavorable. The presence of the metal serves as a lower-energy pathway for gaseous species to first adsorb to the metal and then diffuse on the support surface. This is possible because the adsorbed species attains a lower energy state once it has adsorbed to the metal, thus lowering the activation barrier between the gas phase species and the support-adsorbed species.

Hydrogen spillover is the most common example of an adsorptive spillover. In the case of hydrogen, adsorption is most often accompanied with dissociation of molecular hydrogen (H₂) to atomic hydrogen (H), followed by spillover of the hydrogen atoms present.

The spillover effect has been used to explain many observations in heterogeneous catalysis and adsorption.^[27]

Polymer adsorption

Adsorption of molecules onto polymer surfaces is central to a number of applications, including development of non-stick coatings and in various biomedical devices. Polymers may also be adsorbed to surfaces through polyelectrolyte adsorption.

Adsorption in viruses

Adsorption is the first step in the viral life cycle. The next steps are penetration, uncoating, synthesis (transcription if needed, and translation), and release. The virus replication cycle, in this respect, is similar for all types of viruses. Factors such as transcription may or may not be needed if the virus is able to integrate its genomic information in the cell's nucleus, or if the virus can replicate itself directly within the cell's cytoplasm.

In popular culture

The game of Tetris is a puzzle game in which blocks of 4 are adsorbed onto a surface during game play. Scientists have used Tetris blocks "as a proxy for molecules with a complex shape" and their "adsorption on a flat surface" for studying the thermodynamics of nanoparticles.^[28][29]

See also

• Cryo-adsorption


• Molecular sieve


• Pressure swing adsorption


• Micromeritics


• Kelvin probe force microscope


• Fluidized bed concentrator


• Dual-polarization interferometry


• Polanyi adsorption


• Random sequential adsorption

References

Further reading

External links

Look up adsorption in Wiktionary, the free dictionary.